Basic Electronics for Audio Part 1, who is this Ohm guy anyway?

Anyone who works with audio as a serious hobby or career has been dealing with electronics, whether they know it or not.  From the point where sound is process by a microphone until it enters the air from a speaker, your audio is nothing but a small flow of electrons through wires and is bound by the same rules that govern the power in your house, the battery in your car, or any other electronic device.

When you’re dealing with signal interconnections, levels, and processing it becomes helpful to understand some of the basic laws of electricity.  With this knowledge, you may find a light bulb turning on in your head when you apply your knowledge to gain staging, processing, speaker connections, or troubleshooting signal problems like noise and distortion.

The three basic Electronic properties

Electricity deals with the flow of electrons.  All electrons have a charge and would naturally like to remain at a balanced, neutral potential.  When there’s an imbalance, the electrons will find their way through a conductor in an effort to find that balance.  All electricity flows can be described and calculated with three basic properties.

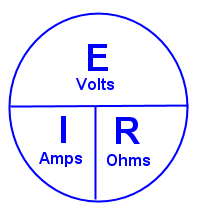
• Voltage
• Current
• Resistance

To use a common water flow analogy, these can be described like this:

Voltage, sometimes called EMF or potential, is the amount of force pushing the electrons, typically expressed with the variable V or E.  This is measured in Volts and equivalent to water pressure in our analogy.
Current is a measurement of how many electrons are flowing, typically expressed with the variable I.  This is measured in Amps and equivalent to the water flow rate, which would be measured in gallons per minute or another quantity over time type measurement.
Resistance, sometimes referred to as impedance, is a measurement of how difficult it is to push electrons through a particular type of material, typically expressed with the variable R.  This is measured in Ohms and is equivalent to the size of the pipe you’re pushing your water through.

So, using the water analogy you can imagine the relationship like this.  The more water pressure, the more water will flow through a given pipe size.  The larger the pipe size the more water will flow through at a given pressure.  This is precisely how we come to Ohm’s Law, solved in it’s three possible algebraic equivalents:

• V=I*R
• I=V/R
• R=V/I

Using this formula, you can find the missing value given any of the other two.   This basic building block leads you to all kinds of more complicated equations, but is really the foundation of all electronics.

What can I use that for?

How about for the signal loss in a cable?  Let’s say we have a line level signal of 1V that we’re going to plug into a pre-amp with a 10k Ohm input impedance.  We can find the current flow required using Ohm’s law, I=1/10,000 or 0.0001 Amp, which would be better referred to as 0.1 milliamp.  So now let’s say that cable we’re trying to use to make the connection has a end to end resistance of 1k Ohm, we could then calculate how much voltage would be lost in the cable due to it’s resistance.  The voltage lost = 0.0001 Amp * 1000 ohms, or 0.1 Volt, meaning if you put 1V into the cable, only 0.9V will make it out the other end.

Where does the voltage go when it’s ‘lost’ in a resistor?

Simple, it disappears as heat.  This heat is measured as power in Watts.  The simple formula is just Voltage multiplied by Current, or P=V*I.  Some algebraic magic on the other Ohm’s law inversions gives you P=I^2*R or P=V^2/R.   The most useful audio piece for this handy little formula is speaker power, since line level signals are so small in voltage and high in resistance and therefore have tiny amounts of power associated with them.

Let’s use this to figure out how much power we can put into a 4 Ohm speaker with a car battery voltage of 12V.  Using Ohms law we have 12V/4 Ohms for 3 Amps of current.  To get to power we have 3 Amps of current and 12 Volts for 36 Watts.  The same result could have been calculated with the formula V^2/R, 12 squared divided by 4 also equals 36 Watts.  At this point I should mention we’re dealing with DC voltage calculations, once you step into Alternating Current, which incidentally ALL audio signals are, the calculations become more complicated, but for now let’s keep it simple.  This little bit of info can come in handy when shopping for car audio parts.  There’s another law that comes into play here too:

Power out of a circuit can never be higher than the power into a circuit

In fact, it’s usually quite a bit lower due to efficiency losses.  So if you’re looking at a little car amplifier that has some crazy 100W per channel output claim, yet only has a 5 Amp fuse on it’s 12V incoming line feed, you can bet that specification is wildly exaggerated, since the amp only has 60W of total power that it can possibly draw.

Ok, now what about Alternating Current?

I did say that ALL audio is actually alternating current, but luckily the basic properties for Ohms law still apply. There’s just a couple other things to define when dealing with simple AC signals:

• Peak level = the maximum voltage in the signal relative to 0 Volts (in one direction only)
• Peak to Peak level = the maximum positive level and the maximum negative level combined
• RMS Level = Root Mean Square, or equivalent power level.  There’s a large amount of math behind this, but the gist is that this is the DC equivalent level, Meaning  10VRMS of AC will heat a given resister exactly as much as 10VDC.  This is a very important measurement as real amplifier power is measured in RMS.

The conversion from peak to RMS is a constant for a simple single frequency sine wave, RMS = 0.707 * peak, and peak = 1.414 * RMS.  Again, I have a disclaimer to mention, audio is definitely not a simple single frequency sine wave, and there’s a little problem with what is called reactance in the calculations.  You may have heard of capacitors and inductors, these mess up the relationship between voltage and current in AC signals and add a whole lot of complication to the formulas.  Generally, you can get pretty far ignoring reactance for basic circuit analysis, particularly for power amplifier outputs, gain staging, and other basic tasks.  Just follow the same Ohms law rules, and be sure to consider that your calculation will be in the same measurement that you started with, for example if you use RMS voltage, you’ll get RMS current.  Resistance stays resistance though, so the Ohms never change at all.

Back to the car amplifier analogy… If you have an amplifier output that can only go from 0 to 12 volts, that means it only has the ability to generate 12 Volts peak to peak into a speaker.  That 12 V P-P translates into 6 V peak, or 6*0.707 volts RMS, which comes out to 4.242.  Using Ohm’s law we can calculate the power into a 4 ohm speaker as 4.242^2/4, or 4.5 Watts RMS.  Pretty weak right?

So how to car audio amplifiers ever get more than 5 Watts?

One method commonly used is called bootstrapping.  This technique basically puts the speaker between two amplifier outputs that are exactly opposite of each other.  This makes the amplifier able to effectively reverse the polarity of the 12V going into the speaker as the signal alternates between positive and negative, and gives double the available voltage to the speaker.  This comes out to a full 24 Volts peak to peak for a equivalent RMS power availability of 18 Watts.  If you add in the fact that while your car is running the battery is actually above 12V due to the alternator charging, you end up with about 14V of power available, 28V peak to peak output, and about 25W RMS of available power.  That is the absolute maximum available with a car’s power source.

But there are amps with way more than 25W per channel out there!

This can be done with a power supply trick, called DC to DC conversion.  The amplifier has a special power supply that can increase the voltage to the range required for much higher power outputs to a speaker.  The power law is still in full effect here though, so these amps have proportionally large current requirements from the battery to produce this kind of real power.  It’s not uncommon for high power car audio amplifiers to draw 10 to 30 or more amps from the battery.  30 Amps would give 360 Watts of power available to the amplifier for translating into the speaker.  Much of that will be lost in the amplifier itself as heat (that’s why they have huge aluminum chassis ‘heat sinks’), but with an average design this amp should provide about 100W RMS per channel into a 4 Ohm load.

There you go… you can now do some basic calculations and call snake oil vendors trying to sell you some crazy million watt amplifier that magically runs off of a AA battery.  Next up, basic circuit analysis.